函数在整个中学阶段占据重要的地位在初中阶段，函数板块包含三类，其中二次函数学习难度最大，深度最高，与高中学段的联系最为密切通常在中考升学考试中二次函数也常常出现在最后一题的位置而在高中学段，函数的重要性更加不言而喻。

在高中新课标中，为了突出函数的重要性，将其单列为一个主线，倡导高中教师依据函数主线开展教学而在我们的日常生活中，也处处离不开函数因为运动无处不在，关系无处不在，所以函数也随处可见，它是刻画我们这一世界的最为重要的模型。

正如克莱因所说，每个数学受教育者都应学会用函数和变量来思考问题“变化中的规律性”，“变化中的不变”是所有函数的共性，在教育教学中我们更应该抓住函数的这一本质特征

《义务教育数学课程标准》指出，“通过初中函数板块学习，应能够探索简单实例中的数量规律和相互关系;并且能结合生活中的实际案例，体会函数概念及表示;结合图象分析函数关系，通过分析，初步讨论变量的变化情况观察分析可知，初中三类函数在课标里的要求都大体相同。

首先理解函数意义，并求解函数解析式;其次，能画出函数图象，并根据参数范围，分类讨论函数变化情况;最后还需体会函数与其他知识的横向关系，综合运用函数知识解决实际问题

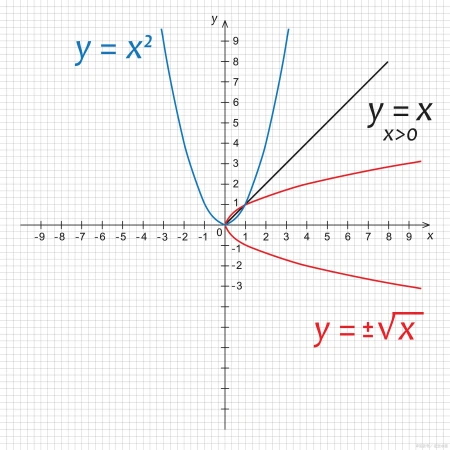
课标特别强化了不同板块知识间的联系，希望通过教材设计帮助学生感悟知识的逻辑顺序和实质联系，通过螺旋上升、层层递进的过程，促进学生不断深入对函数的理解教材根据课程和学生的实际情况，分三个阶段开展函数内容学习。

首先.让学生在实例中感受到事物的变化，以及事物变化中的不变性，找到规律，形成感性认识;随后在初步认识后，用数学语言归纳得出定义，研究函数性质，了解基本方法，并运用方法解决问题;最后，强化二次函数知识纵向的整体性和横向的关联性，探索函数与其他数学知识之间的关联，让学生对函数的价值和意义有更加深刻的认识。

在教学时应总结形成研究函数的具体通法，让学生从研究的思维了解函数注重知识的整体性与关联性，可将函数内容与方程、不等式的内在联系分析给学生在进行具体教学时，可采用问题驱动的方式，通过问题激发学生思考，引导学生步步探索；教学中教师应善用多媒体辅助教学，在二次函数图象分析时，借助几何画板呈现函数图象;在日常教学中，通过PPT呈现知识结构网络，帮助学生建立对函数的直观认识与理解。

函数单元目标为：探索实际例子中的数量关系以及规律，体验探索、分析、建立变量间关系的过程，进一步培养数学抽象素养，并能根据已知条件求解函数表达式;能画出函数图象，体会其与表达式的关系，能根据表达式探索图象性质与变化情况，发展探究精神;运用函数知识解决简单的实际问题;经历从具体情境中抽象出函数概念的过程，并结合图象分析各类情境中的函数关系，发展数学建模素养;体会函数与生活的密切联系;体会函数与其他知识的横向联系，能运用图象求解方程，体会数形结合思想，发展运算与直观想象素养;感受知识的关联性与整体性。

学生若能根据不同情境找到函数模型，并依据题目条件求出函数表达式;能按照列表描点连线步骤，画出函数图象，同时根据函数图象从单调性、对称性等维度有策略地探究函数性质;能在复杂现实情境中建立数学模型，运用函数模型解决生活问题;能够清晰指出函数与其他相关知识的联系与区别并利用图象直观解决方程和不等式问题，说明函数单元教学目标已经达成。

要发展学生核心素养，教学设计中需要保证知识的整体性和关联性整体性是指知识体系的逻辑关系要严密可迁移，关联性包含横向关联与纵向关联，强调知识的内部联系可按主线进行教学设计，基本路径是总体设计、分阶段、按课时实施，深入挖掘知识之间的关联，总结教学方法与思想，通过知识的单元教学，减少碎片化，帮助学生梳理形成知识结构。